Los Curris

¡Hola a todos!

Advertencia: este post es una ida de olla - si queréis cosas sesudas, buscad en otro sitio.

Lo habría titulado "Método simple para hacer más sencillo cualquier juego en el que puedas escribir (y se use) tu nombre".

Es un método sencillo, compuesto por 4 pasos:

1. Ejecutad el juego.


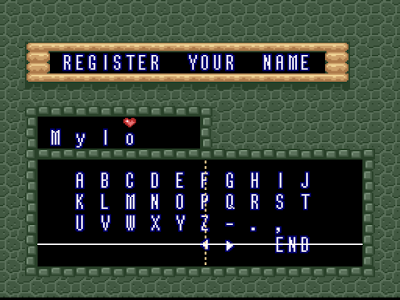
2. Cread un jugador nuevo para comenzar una nueva partida, o cambiad el nombre del que ya estéis usando si el juego lo permite. Mirad más abajo para ver el nombre que hemos escogido como ejemplo.


3. ¡Comenzad a jugar con recientemente creado!


4. Si habéis seguido bien los pasos del ejemplo, ¡todos los personajes del juego os llamarán con ese nombre, incluidos los monstruos!


El caso es que incluso los jefes finales os llamarán así. ¡Esto les hará parecer mucho más débiles, y os brindará una ventaja psicológica muy importante!

Algunos ejemplos de nombres a usar: MyMaster, ImAss, HitMe... en fin. Los juegos modernos permiten poner nombres largos, con apellidos. ¡Dad rienda suelta a la creatividad! Y por supuesto, no os olvidéis de adaptar el nombre al idioma en que esté el juego.

Por último, un apunte: esta táctica puede funcionar mal en los juegos multijugador. El resto de los jugadores puede acabar por pillaros manía.

¡Este ha sido mi consejo!
(hu-ha!)

Hola amigos!

Uno rapidito hoy.

Todos recordamos algún momento que habríamos preferido disfrutar a cámara lenta. Con este pensamiento en la cabeza, me dije "voy a ver si encuentro unos cuantos vídeos chulos en slow motion en youtube, los junto y los pongo en el blog"...

Pues no he tenido que buscar mucho; ya el primero que me salía era simplemente buenísimo.


Sé que es un poco largo (6 minutos). Al menos mirad al tío que le da un cabezado a un globo azul en el segundo 1:34... la mayoría son así de buenos.

Y hay muchas explosiones. Las explosiones molan.

Ah y la musiquilla de fondo mola bastante. Si alguien sabe cuál es, por favor que me lo diga.

Y no quería despedirme sin transmitiros la frase que he oído hace un rato:

"En mi planeta tenemos un dicho: Existen maneras de morir... y maneras de morir"

¡Buenas noches!

Aunque parezca que, dado mi reciente cumplimiento de edad, voy a hablar de lo viejo y deprimido que me siento, no va a ser así. Tampoco voy a hablar de la primavera que ya comienza.

Voy a hablar de números.

Como siempre, trataré de poner el menor número posible de fórmulas. Creo firmemente que puedo salirme con la mía sin escribir ninguna esta vez. Aunque tendré que escribir algunos Números Realmente Grandes.

Cuando estudiaba (hace ya muchos años! jejeje - qué viejo me siento ^^) tuve una experiencia interesante: llevaba mucho tiempo dándole vueltas a un juego en mi cabeza - el juego de las torres de Hanoi.

Seguramente habéis oído hablar de él; tenemos tres palitos verticales, y unos discos de diferentes tamaños engarzados el primero de ellos, estando los discos más pequeños encima de los más grandes. El juego consiste en pasar todos los discos del primer al tercer palito siguiendo 3 reglas sencillas:

• solo se puede mover un disco cada vez
• nunca debe haber un disco más grande encima de otro más pequeño
• se puede usar el segundo palito como "auxiliar", pero cumpliendo las reglas anteriores
  

De hecho no hacen falta los palitos; vale con poner unas fichillas de tamaños diferentes, y que se dejen apilar. Aquí va un ejemplo (cortesía de la wikipedia) con 4 discos. Imaginaros los palitos, si os resulta más fácil

El caso es que yo llevaba bastante tiempo dándole vueltas a este juego. Cuando me aburría en alguna de mis clases, lo que, por desgracia, ocurría muy a menudo (no tanto por la falta de pericia profesional de mis enseñantes sino más bien por la poca fuerza de voluntad del que suscribe) me ponía a hacer dibujillos en un papel con 3, 4, 5 o más discos. Y bueno, digamos que dibujé bastantes folios. Sobre todo en una parte especialmente aburrida (procesos recursivos) de una asignatura de Matemática Discreta.

El caso es que llegó la época de exámenes. Entre ellos el de Matemática Discreta. Yo no había estudiado mucho ni había prestado demasiada atención... y sin embargo, ¡me preguntaron sobre las Torres de Hanoi!

No cupe en mí de gozo. ¡A bordarlo!

Recuerdo que se nos exigía averiguar el número mínimo de movimientos de disco que hay que hacer para mover una pila de n discos (de una forma adornada; se mencionaba que unos monjes jugaban con 64 discos en un templo y la profecía decía que cuando se colocara el último disco se acabaría el universo; se pedía calcular la edad del universo). Curiosamente, había que aplicar la fórmula de los procesos recursivos ... a la que yo no había prestado atención ...

No me preguntéis cómo, pero conseguí deducir el número yo mismo. No se me olvidará nunca la solución: para n discos, hacen falta como mínimo 2ⁿ-1 movimientos (vale, me habéis pillado. Eso de ahí delante es una fórmula. Sorry.). Y eso es un montón. Los monjes tendrían que hacer ¡18446744073709551615 movimientos! para que se acabara el mundo; Suponiendo unos monjes que hicieran un movimiento por segundo y sin equivocarse - unos monjes con linux y coprocesador matemático - eso serían, redondeando, algo más de 585942 billones de años (584.942.417.355 años, 26 días , 17 minutos y 30 segundos. He ignorado los años bisiestos - pero pilláis la idea)

Parece mentira que 64 disquitos y 3 reglas sencillas den lugar a un número tan grandísimo.

Pero el caso es que hay un montón de ejemplos así. Está el conocido ejemplo del tablero de ajedrez - coges un granito de arroz por el primer cuadro, 2 por el segundo, 4 por el tercero, 8 por el cuarto etc etc... cuando llegas al último coges 2⁶⁴ granos de arroz y luego lo flipas con la paella que te va a salir.

En realidad, cuando empiezan a salirte "cosas elevadas a cosas", la cosa se pone interesante. O bien elevas a cantidades muy muy pequeñas, o bien te van a salir números monstruosamente grandes.

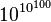Dicho esto, dejadme presentaros el número más grande "con nombre" (como el millón, billón, etc): el gogolplex. Equivale a , o lo que es lo mismo:


Es mucho mucho mucho.

Y sí, hace poco pusieron un post parecido en ion litio, pero ellos no hablaban de mi examen.

Un saludín.

(nota: las imágenes del googolplex también son copiadas de la wikipedia)

Hoy, al ir a comprar unos pastelitos para compartir con mis compañeros de oficina por motivo de mi natalicio, me ha parado una señorita con un micro y un señor con una cámara. Trataré de reproducir la conversación lo más fielmente posible:

- Hola, ¿Te podemos hacer un par de preguntas? Será un momentito
- Vale
- ¿Qué haces con la comida del frigorífico que te sobra, por ejemplo, el pollo?
- Bueno, a veces tiro alguna cosa, pero uso el congelador. Congelo el pollo.
- Estupendo, muchas gracias.
- De nada, adiós!

Mientras se alejaban, oí que la mujer le decía al cámara algo como "ha quedado bien, lo del pollo".

Me dí prisa en volver porque había tardado mucho, así que ni pregunté de qué canal y programa eran.

Más tarde, habiendo salido de trabajar, mi hermano Rodrigo acababa de llamarme para felicitarme por mi cumpleaños, desde la casa de un amigo. Justo cuando hemos terminado de hablar, ¡he aparecido en la tele de su salón!

Señoras, señores y frikis todos.

Hoy cumplo un año más. Apenas han pasado unos minutos y ya me siento una marea de experiencia y responsabilidad recorriendo mis sinapsis y volviéndome una persona mucho más seria, cuidadosa, paciente y observadora.

...

¡Que nooo!

Hoy se me ha ocurrido hacer unas cuantas efemérides. Sobre el día de mi venida a este planeta.

Cosas que pasaron el 13 de Marzo:

• Es un día Astronómicamente interesante: en 1781, Ser William Herschel descubrió Urano. Ese Mismo día, pero en 1930, Clyde Tombaugh descubrió Plutón.
• En 1960 nace ¡Fito Paez! y tres años más tarde Adam Clayton, de U2.
• Televisión Española realizó su primera retransmisión, la de una corrida de toros.
• También es una fecha de descubrimientos: En 1519 Hernán Cortés pisa Méjico por primera vez, mientras que en 1975 se lanzó la nave espacial Soyuz T15.
• También está la tristemente habitual dosis de sangre: matanzas de niños escoceses en 1996, toma de 70 rehenes en holanda en 1978, asesinato de un zar en 1881...
• El primer strip-tease profesional tuvo lugar el 13 de Marzo de 1894 en el Divan Fayonau Music Hall en París.

Mi abuela lo habría dicho de esta forma: "se conoce que es menester organizar alguna cosilla". Tomo prestados sus vericuetos verbales para invitaros a pasaros por mi casa el próximo viernes 16, que ya no será mi cumpleaños pero que en fin.

El inicio del evento será a las 22 horas. Yo pongo la comida y el ron, hielo, limón y hierbabuena. Los que seáis de whisky u otros brebajes por favor traed vuestras bebidas espirituosas. Tomaremos un piscolabis y luego nos iremos a algún lugar de la avenida de Brasil. El lugar está aún por determinar; en esa zona no suelen ser muy exigentes con la ropa, pero procurad ir vestidos de forma que no os digan "no tengo suelto".

Como si queréis venir disfrazados - con tal de que vengáis, me da igual.

Vuestra presencia y buen rollito será el mejor regalo que me podéis hacer; no preciso regalos adicionales. ¡Así que no utilicéis la excusa de no haberme comprado un regalo para no venir! (triple negación =))

Ah y tampoco hace falta que me cantéis una canción. Pero si alguien se atreve...


Un saludo majetes, y gracias!

Hoy un vídeo.

Seguramente todos lo habéis visto ya, porque sois unos frikis (de otra forma la cabecera del blog os habría espantado).

Me encanta el siguiente vídeo porque versiona una canción ochentera utilizando la película friki por excelencia, LOTR (Compartiendo trono con Star Wars, vale)


Es un poquillo más soez de lo que pongo habitualmente, como corresponde al metal castizo. Tenéis más en la página del autor, el Reno Renardo.

¡Tened la mente abierta y disfrutadlo!

(¡Gracias yisas por mandármelo!)

Hola amigos!

Como la mayoría ya sabéis, he estado de vacaciones dos semanitas.

La primera semana la pasé en los carnavales.


El traje que llevo es un traje de verdad de los marines americanos... lo compré por e-bay a un vendedor de excedentes del ejército. No es que apoye lo que hacen, pero me apetecía. Solo tengo 4 fotos en mi cámara de todos los carnavales; cuando me pasen las demás (que se hicieron con otra cámara) veré si puedo mejorar ésta.

En cuanto a Budapest... no puedo escribir aquí todo lo que me ha pasado, sería muy largo. Pero daré algunas pinceladas

• Budapest es una ciudad muy bonita, pero de lejos. De cerca uno ve la suciedad y los problemas demasiado rápido.
  
• Tienen demasiados restaurantes de comida rápida.
• Las chicas de Budapest no me parecieron tan guapas.
• El húngaro es dificilísimo! Yo aprendí a decir "Si", "No", "Gracias", "Calle" y "Cosa". No me atreví a preguntar sobre los insultos (mi táctica habitual) porque "Gracias" ya me sonaba suficientemente ofensivo (se pronuncia "Keszenem", pero las únicas vocales que tiene son tres oes)
• El metro tiene voz de hombre, el tranvía de mujer.
• Tienen un campus universitario curradísimo. La escuela de informática tiene el edificio más grande del campus, como debe ser.
• Es barato. Ha sido la primera vez que he gastado exactamente lo que tenía pensado gastar desde el principio. O puede que sea que ya me estoy haciendo viejo y tengo más experiencia.

Bueno, si queréis ver más cositas, aquí os dejo mi álbum de fotos sobre el viaje. La mayoría de las fotos tienen comentarios graciosetes o curiosos... echadles un ojo!

Un saludo, es un placer estar con todos vosotros de nuevo!